Фрактал Ляпунова

Фрактал Ляпунова (также известный как фрактал Маркуса-Ляпунова) — бифуркационный фрактал, порождённый расширением логистического отображения, в котором степень роста совокупности r периодически меняет значение с A на B и наоборот.

Логистическое отображение является одним из наиболее кратких математических представлений о росте населения. В зависимости от скорости плодовитости, используемой на диаграммах, оно будет генерировать либо нейтральную систему, либо устойчивую колебательную систему, или хаотическую систему. Чтобы определить, какой из этих результатов произойдет, математик Александр Ляпунов разработал значение называемое экспонентой Ляпунова. Это полезный индикатор, потому что, для логистического отображения:
♦ Если экспонента Ляпунова равен нулю, изменение численности популяции является нейтральным: численность популяции остается постоянной, фиксированной точкой.
♦ Если экспонента Ляпунова меньше нуля, популяция становится устойчивой. Чем меньше число, тем быстрее население стабилизируется.
♦ Если экспонента Ляпунова положительна, население станет хаотичным
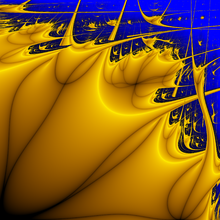
Ученый Марио Маркус визуализировал экспоненту Ляпунова как показатель перемещения популяции между двумя темпами роста. Таким образом, он создал графическое пространство с одной скоростью роста измеряемой вдоль оси Х и другой вдоль У. Для любой точки (х, у) есть конкретное значение экспоненты Ляпунова, которое описывает поведение популяции. Маркус создал цветовую схему для представления экспоненты. Один цвет представляет положительные значения, а другой – отрицательные и нуль. Второй цвет он представил градиентом от светлого к темному, так что меньшие отрицательные числа светлее, а те, что ближе к нулю – темнее.

• Рассмотрим изображение. Синий фон отображает все точки, где комбинации темпов изменения на осях Х и У приведут к хаотическому росту численности популяции. "Плавающие" желтые фигурки показывают, где популяция будет стабилизироваться. Чем светлее желтый, тем стабильнее популяция.

Стандартный логистический фрактал Ляпунова с итерационной последовательностью AB в области [2, 4] x [2, 4].

Обобщённый логистический фрактал Ляпунова с итерационной последовательностью BBBBBBAAAAAA; зона роста параметра - в области [3.4, 4.0] x [2.5, 3.4]. Также известен как Zircon City.

Рассмотрим изображение справа, показывающее в увеличенном масштабе участок основного изображения выше. Здесь мы видим несколько фигур, которые повторяются в меньших итерациях.

Увеличение участка Zircon City, демонстрирующее самоподобие

1. Выбрать строку из символов A и B любой нетривиальной длины (например, AABAB)
2. Построить последовательность S последовательных символов строки, повторённых необходимое число раз.
3. Выбрать точку (a,b) принадлежащую [0,4]Χ[0,4]
4. Определить функцию r_n=a если S_n=A , и r_n=b если S_n=B
5. Принять x₀=0.5 и выполнить итерации x_n+1=r_nx_n(1-x_n)
6. Вычислить экспоненту Ляпунова:
   
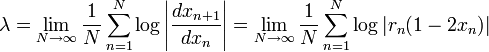
7. Раскрасить точку (a,b) согласно полученному значению λ
8. Повторить шаги 3-7 для каждой точки плоскости изображения.

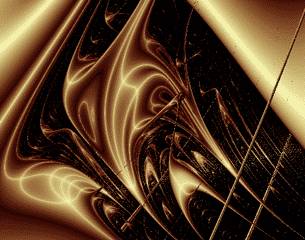
в данном случае хаос окрашен в черный цвет, а стабильность в золотистый