Колыбель Ньютона (маятник Ньютона) — механическая система, названная в честь Исаака Ньютона для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо, поскольку колебания маятника совершаются под действием силы тяжести, силы упругости и силы трения.

Это изобретение, придуманное Саймоном Пребблом в 1967 году, а сегодня часто встречаемую на письменных столах в кабинетах и офисах, можно поместить и в музей физики. Знание того, что она иллюстрирует законы сохранения импульса и сохранения энергии не только не помешает, но и придаст особый смысл наблюдению.
При отклонении первого шарика данной системы и последующим его возвратом к изначальному положению, его энергия и импульс передадутся без изменения через три средних шарика последнему, который приобретёт ту же скорость и поднимется на ту же высоту. Он в свою очередь передаст свой импульс и энергию по цепочке снова первому шарику. Крайние маятники будут колебаться, а промежуточные будут неподвижны. Из-за потерь механической энергии вследствие работы сил трения и упругости колебания маятников затухают, так как в реальных механических системах всегда действуют диссипативные силы.
Чтобы найти скорости шаров после упругого столкновения, надо записать уравнение закона сохранения импульса для такой системы и уравнение закона сохранения энергии и решить полученную систему уравнений. Результат известен: движущийся шар останавливается, а покоящийся приобретает скорость первого.
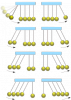
В колыбели Ньютона первый шарик передаёт импульс второму шарику и останавливается. Второй шарик получает импульс потенциальной энергии от первого, но из-за невозможности преобразования потенциальной энергии в кинетическую, импульс переходит от второго маятника далее — в третий, четвертый, пятый. Последний шарик не имеет перед собой, кому передать свой импульс, поэтому свободно движется, поднимаясь на высоту h, затем возвращается, и всё повторяется в обратном направлении.