Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
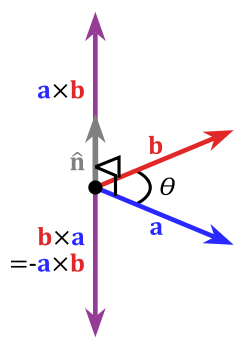
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Определение:
Векторным произведением вектора a на вектор b в пространстве R3 называется вектор c, удовлетворяющий следующим требованиям:
длина вектора c равна произведению длин векторов a и b на синус угла φ между ними:
|c|=|a||b|sin φ;
вектор c ортогонален каждому из векторов a и b;
вектор c направлен так, что тройка векторов abc является правой;
в случае пространства R7 требуется ассоциативность тройки векторов a,b,c.
Обозначение:
c=[ab]=[a,b]=a × b
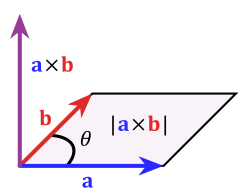
Рис. 1. Площадь параллелограмма равна модулю векторного произведения
Геометрические свойства векторного произведения:
Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
Модуль векторного произведения [ab] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b (см. рис.1).
Если e — единичный вектор, ортогональный векторам a и b и выбранный так, что тройка a,b,e — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
[a, b]=S e
Рис.2. Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений
Если c — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, e — единичный вектор, лежащий в плоскости π и ортогональный к c,g— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула:
[a, c]=Prea•|c|g
где Prea проекция вектора e на a
|c|-модуль вектора с
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c. Такое произведение трех векторов называется смешанным.
V=|a•(b×c)|
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
V=a×b•c=a•b×c
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Выражение для векторного произведения в декартовых координатах
Если два вектора a и b определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
a=(ax,ay,az)
b=(bx,by,bz)
а система координат правая, то их векторное произведение имеет вид
[a, b]=(aybz-azby,azbx-axbz,axby-aybx)
Для запоминания этой формулы :
[a,b]i=∑εijkajbk
где εijk— символ Леви-Чивиты.




