Допустим нам дана задача - построить правильный n-угольник. Правильным многоугольником считается тот, у которого все углы равны и все стороны равны.
Алгоритм очень прост.
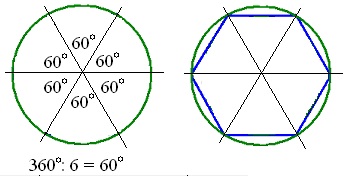
Центральный угол окружности составляет 360º.
1. Делим 360º на n равных частей.
2. Проводим лучи до пересечения с окружностью.
3. Соединяем точки пересечения.
Полученный многоугольник является правильным n –угольником.
Следующий алгоритм построения правильных многоугольников основан на свойствах описанной окружности около правильного многоугольника и вписанной в правильный многоугольник.
Теорема 1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
Теорема 2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствие 1. Окружность, вписанная в правильный многоугольник, касается
сторон многоугольника в их серединах.
Следствие 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот многоугольник
Для построения правильных n – угольников при n › 4 обычно используется окружность, описанная около многоугольника.




