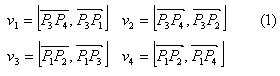Построения на плоскости (2D)

Псевдоскалярным (или косым) произведением векторов a и b на плоскости называют число

a ∧ b = |a|•|b|• sin(φ),

где φ - угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов нулевой, то полагают a ∧ b = 0.

Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

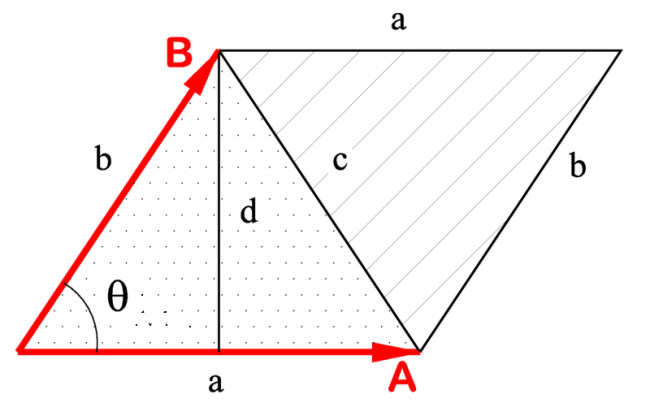
С её помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.

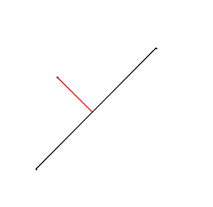
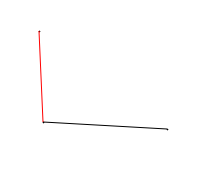
Расстоянием от точки до отрезка является либо перпендикуляр, опущенный из этой точки на отрезок, либо минимальное расстояние от точки до одного из концов отрезка.

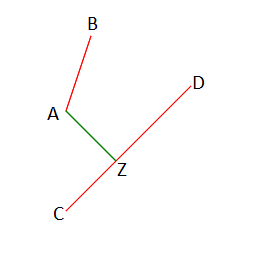
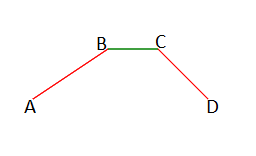
Координаты концов первого отрезка: A(x_a, y_a), B(x_b, y_b).
Координаты концов второго отрезка: C(x_c, y_c), D(x_d, y_d).

Для начала проверим не пересекаются ли отрезки.

Общая информация
Интерполирование по Эрмиту есть специальный вид многоинтервальной интерполяции, при котором интерполирующий многочлен H_n(х) обеспечивает не только равенство H_n(х) значениям f(x), но и совпадение некоторого количества производных в узлах интерполяции.
Многочлен Эрмита единственный, это следует из однозначности его построения.
Остаточный член интерполяционной формулы Эрмита равен:

Спрайтовая анимация — одна из тех вещей, которые при всей своей примитивности успешно работают и применяются в компьютерной графике и играх уже больше четверти века. Даже в трехмерных играх есть спрайты — например, билборды взрывов. Во многих браузерных и флеш-играх применяют именно спрайтовую анимацию, так как она очень проста и не требует высокой производительности — просто переключай кадры и все!

Кривые Безье

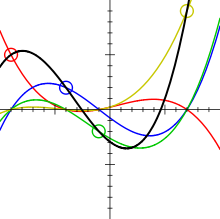
Кривые Безье используются в компьютерной графике для рисования плавных изгибов, в CSS-анимации и много где ещё.
Несмотря на «умное» название – это очень простая штука.
В принципе, можно создавать анимацию и без знания кривых Безье, но стоит один раз изучить эту тему хотя бы для того, чтобы в дальнейшем с комфортом пользоваться этим замечательным инструментом. Тем более что в мире векторной графики и продвинутых анимаций без них никак.

Виды кривых Безье

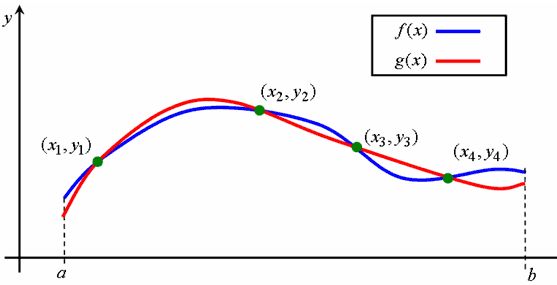
Многочлен Ньютона интерполяционный – как и другие интерполяционные формулы, служит для построения многочлена n-й степени, который совпадает в (n+1) точке co значениями неизвестной искомой функции у = f(x).

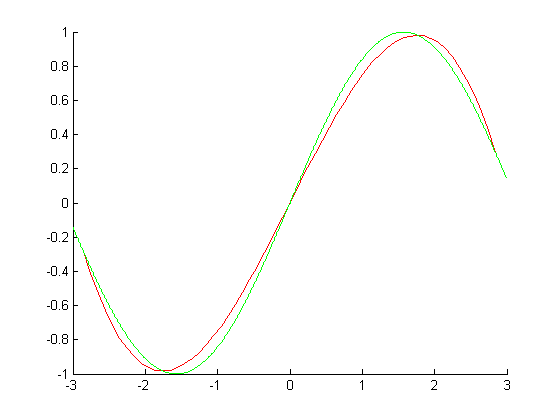
Общий смысл интерполяции

Решение задачи методами интерполирования предполагает выполнение условия P(x_i)=f(x_i) при x из [a;b] (1)
Интерполяционный алгебраический полином имеет вид P_n(x) = Sum(a_ixⁱ) где i=0,1,..,n (2)

Определение интерполяции

Пусть даны два отрезка. Первый задан точками P₁(x₁;y₁) и P₂(x₂;y₂). Второй задан точками P₃(x₃;y₃) и P₄(x₄;y₄).

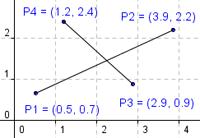
Взаимное расположение отрезков можно проверить с помощью векторных произведений: