Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
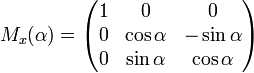
Вращение вокруг оси y:
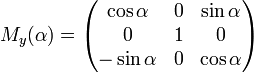
Вращение вокруг оси z:
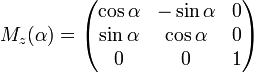
После преобразований мы получаем формулы:
По оси Х
x'=x;
y':=y*cos(L)+z*sin(L) ;
z':=-y*sin(L)+z*cos(L) ;
По оси Y
x'=x*cos(L)+z*sin(L);
y'=y;
z'=-x*sin(L)+z*cos(L);
По оси Z
x'=x*cos(L)-y*sin(L);
y'=-x*sin(L)+y*cos(L);
z'=z;
Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).





Комментарии
Здравствуйте. Спасибо за полезную инфу про уравнения а не матрицы. Во всём интернете только матрицы.
У Вас опечатка в уравнении вращения по Z в координате Y= надо минус добавить
И ещё. Все предыдущие уравнения можно подставить в последнее уравнение при вращении по Z. И не надо столько писанины. На самом деле самый простой и убогий способ вращать вектор во вращающейся системе координат.
И Вам спасибо.
Это вращение по мировым осям ? Если да то как сделать по осям объекта ?
Задавайте объект в мировых координатах. Вращайте его относительно мировой системы координат. А при отрисовке преобразуйте в экранные координаты. Посмотрите пример преобразования в экранные координаты.
просто я не так понял, здесь мы вращаем точки куба что вращает сам куб.
Мне нужно вращать просто 3д объект , данный способ не подходит