Фрактал Дракон Хартера-Хейтуэя

Дракон Хартера, также известный как дракон Хартера — Хейтуэя, был впервые исследован физиками NASA — John Heighway, Bruce Banks, и William Harter. Кривая дракона принадлежит к семейству некоторых фрактальных кривых, которые могут быть получены рекурсивными методами. Дракон Хартера был описан в 1967 году Мартином Гарднером (Martin Gardner) в колонке «Математические игры» журнала «Scientific American». Многие свойства фрактала были описаны Чандлером Девисом и Дональдом Кнутом.

Фрактал может быть записан как L-система с параметрами:
• угол равен 90°
• начальная строка — FX
• правила преобразования строк:
• X X+YF+
• Y -FX-Y

Для его построения возьмем отрезок. Повернем его на 90 градусов вокруг одной из вершин и добавим полученный отрезок к исходному. Получим уголок из двух отрезков. Повторим описанную процедуру. Повернем уголок на 90 градусов вокруг вершины и добавим полученную ломаную к исходной.

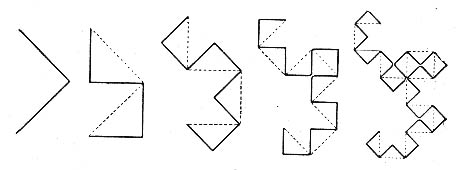
Повторяя названные действия и уменьшая ломаные, будем получать все более сложные линии, напоминающие фигуру дракона.

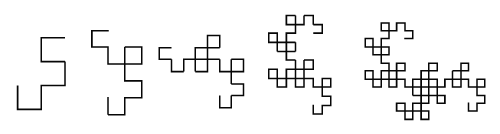
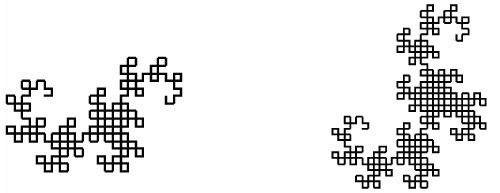
Пример алгоритма на delphi:

procedure Dragon(x1,y1,x2,y2,Depth:Longint;canv:TCanvas);
  procedure Paint(x1,y1,x2,y2,k:Longint);
  var tx,ty:Longint;
  begin
   if k=0 then
    begin
     canv.MoveTo(x1,y1);
     canv.LineTo(x2,y2);
     Exit;
    end;
   tx:=(x1+x2) div 2+(y2-y1) div 2;
   ty:=(y1+y2) div 2-(x2-x1) div 2;√
   Paint(x2,y2,tx,ty,k-1);
   Paint(x1,y1,tx,ty,k-1);
  end;
begin
 Paint(x1,y1,x2,y2,Depth);
end;

Можно увидеть «повторения» в кривой дракона. Очевидно, что рисунок повторяется по той же схеме, с наклоном в 45 ° и коэффициентом сжатия равном корню из двух. Таким образом, точки сгиба образуют логарифмическую спираль. Фрактальная размерность кривой:

Что относит её к кривым Пеано.
Кривые дракона обладают еще одним интересным свойством: при совмещении нескольких из них, они не пересекаются, создавая потрясающие узоры.

Кривая драконы-близнецы, также известная как дракон Девиса-Кнута, может быть построена путем размещения двух кривых дракона "спиной к спине".

Кривой Леви, также приписывают схожесть с драконом, иногда называя её драконом Леви.