Операции преобразования на плоскости

Для описания произвольного перемещения фигуры на плоскости необходимо рассмотреть несколько простейших движений, таких как параллельный перенос, поворот относительно оси и зеркальное отражение относительно оси и точки (полюса), потому что любое сложное движение всегда можно представить как совокупность простых движений.

Параллельный перенос
Параллельный перенос на вектор переносит точку M(x,y) в точку M'(x',y'). При этом координаты точек будут изменяться на величину проекции вектора параллельного переноса на соответствующую ось

x' = x + a_x , y' = y + a_y. (1)

При параллельном переносе отрезок перемещается параллельно самому себе, его длина и ориентация не изменяется (рис.1).

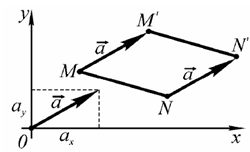
Рис.1. Параллельный перенос

Демонстрация параллельного переноса на JS

Поворот
Поворот точки вокруг координатной оси против часовой стрелки на угол χ (рис. 2а) изменяет координаты точки таким образом, что расстояние от точки до начала координат не изменяется:
x′ = x cosχ − y sinχ,
y′ = x sinχ + y cosχ. (2)

При повороте отрезок не изменяет своей длины, а также не изменяются углы между совместно поворачиваемыми отрезками (рис. 2а).
Если необходимо выполнить поворот относительно произвольной точки, несовпадающей с началом координат, то сначала выполняется параллельный перенос полюса и поворачиваемого объекта на вектор a, при котором полюс совпадет с началом координат. Затем выполняется поворот, а затем параллельный перенос на вектор (-a ) (рис. 2б).

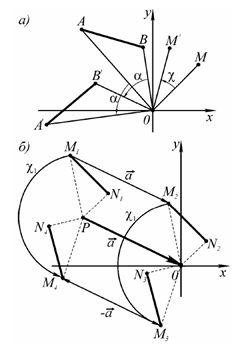
Рис.2. Поворот точки и отрезка

Демонстрация поворота фигуры на JS

Отражение
Зеркальное отражение относительно оси абсцисс (рис. 3) приведет к тому, что координата x точки не меняется, а координата y меняет знак на противоположный
x' = x, y' = - y . (3)
При отражении относительно оси ординат знак меняется у координаты x , а у координаты y знак не изменяется
x' = - x, y' = y . (4)
Отражение относительно начала координат изменяет знаки на противоположные у обеих координат:
x' = - x, y' = - y . (5)
В том случае, если отражение производится относительно произвольной оси, то до выполнения отражения необходимо будет выполнить параллельный перенос объекта и оси на вектор a так, чтобы ось отражения совпала с одной из координатных осей, затем выполнить отражение, а после этого выполнить параллельный перенос на вектор (− a).
При отражении относительно произвольного полюса вначале выполняется параллельный перенос, совмещающий полюс с началом координат, затем отражение относительно начала координат и после этого параллельный перенос для возврата полюса в первоначальное положение.

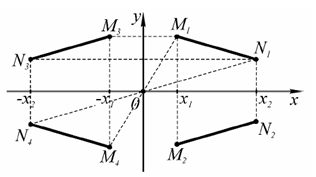
Рис.3. Отражение относительно оси и полюса.

Масштабирование и деформация
Кроме перемещений объекта по поверхности его можно деформировать. В случае если деформация будет пропорциональной, то ее можно рассматривать как масштабирование объекта. При деформации объекта координаты его точек изменяются на некоторую константу
x'= αx, y' = βy . (6)

Если α=β, то деформация будет пропорциональной (масштабирование (рис.4)). Если константы α и β будут положительными, то производится только деформация, а если отрицательными, то кроме деформации происходит еще и отражение.

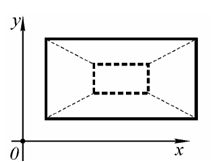
Рис.4. Масштабирование прямоугольника

Демонстрация масштабирования фигуры на JS